Abstract

Shashiko comes, not from the imperial courts, but from the humble origins of rural Japan. This textile tradition requires only needle, thread and countless hours of patient stitching. No fancy machinery or clever devices are used. It is just cloth, single or layered, held together by running stitches. The results are beautiful: geometric patterns interlock with precision and grace, stunning tessellations emerge. Some of the traditional patterns are easy to decipher but others are less obvious. This paper will examine how these patterns are drawn on the cloth and what design principles the stitcher uses to guide the needle.

1. Background

1.1 Origins of the technique. Peasant farmers and fisherman knew how to be frugal. Cloth and thread were precious in pre-modern Japan and garments were carefully patched and reinforced to extend their useful life. At first repairs were done with the same fiber dyed the same color. Efforts were made to camouflage the patch and make it blend in. Often the damaged cloth was of indigenous hemp or other local bast fiber dyed deep blue with indigo. Winters in Japan can be severe, especially in the North. To better fend off the chill and piercing wind, peasants donned layers of clothing and quilted clothing.

1.2 White, cotton thread. Cotton arrived in Japan in the 1300s and 1400s: it was an exotic, expensive foreign good, and only the aristocracy had sufficient wealth to make an ostentatious display of it. In the 1700s it became more prevalent but still was considered a status thread. By the 1800s white cotton thread became more commonplace and gained great popularity in the countryside. Instead of trying to hide the stitch, sewers in the 18 th and 19 th century drew attention to them. They made nets of fine white stitches arranged in regular overall geometric pattern floating on seas of midnight blue. The contrast and the aesthetic of white on blue or blue on white became a folk tradition. Many of the traditional geometric patterns refer to and are stylizations of the natural world. They have names like pine bark, mist, blowing pampas grass and tortoise shell. Like characters in Kanji, they are echoes of abstracted pictographs, reduced to the bare essentials. The steady, predictable rhythms make a quiet beauty and serenity.

2. Patterns Made with Overlaying Sets of Parallel Lines

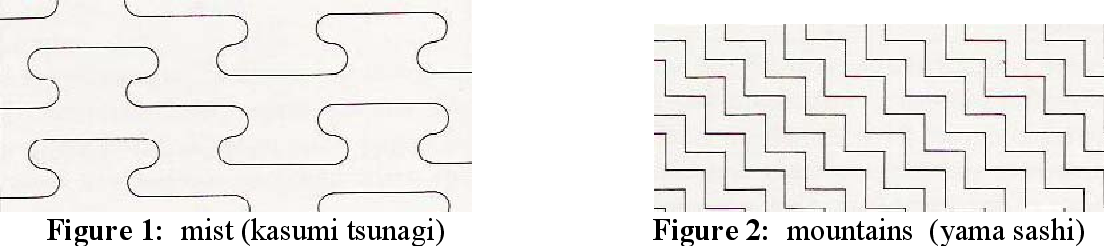
1.1 Types of grids. A few of the patterns are made from simply parallel lines. The lines bend or turn sharp corners but never intersect. Their spacing adds to the rhythms. There is a snap-to-the-grid adherence. The grid can be squares, or equilateral triangles of isometric graph paper. The line of running stitches follows and matches the grid. Quilters fondly refer to this as ‘stitch in the ditch’. Patterns like mist and mountain are formed from these parallel lines.

 

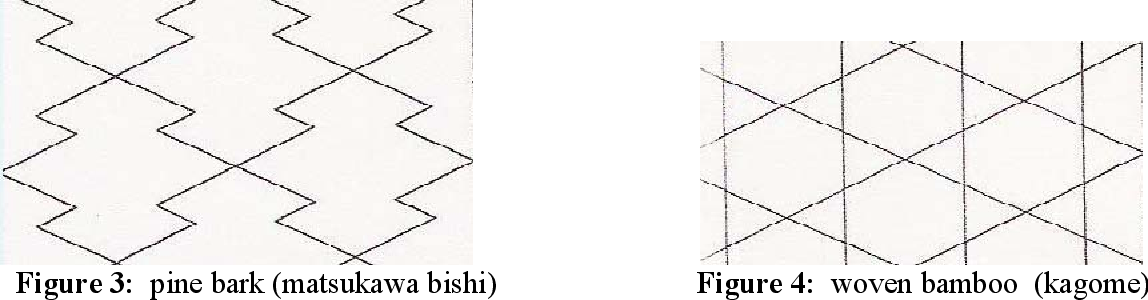
1.2 Intersecting sets of parallel lines. Patterns like Straight Feather, Basketweave, Fish Scales, Pine Bark, and Woven Bamboo overlays grids of parallel lines. Again the layout grid is obvious. The stitcher marks the fabric with guidelines. She then sews sets of parallel lines. The pattern emerges when the eye sees the intersections. Quilters fondly refer to this as ‘stitch in the ditch’.

 

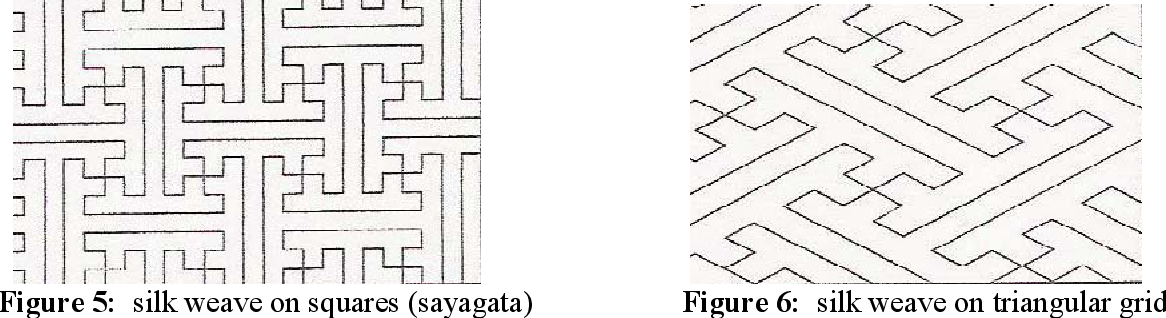
1.3 Motifs that conform to either grid. Sometimes a motif can be drawn in two ways, locked to the square or isometric grid. The convoluting lines of running stitches still follow to the ditch, but the grid itself becomes a series of pivot points. The overall results may look like interlocking motifs, but it is achieved by stitching maze-like lines that jig and jog but eventually reach the opposite side. The Silk Weave and the Cypress Fence are based on both grids.

 

3. Patterns Made by Grid Lines, Connecting Lines, and Pivot

3.1 Hydrangea motif. The hydrangea motif is based on the square grid. A network of carefully drawn crosses, evenly spaced with line segments of equal length is the foundation. These lines are the grid lines. From the center of the crosses, short, connecting lines are sewn to make the diamond shapes.

 

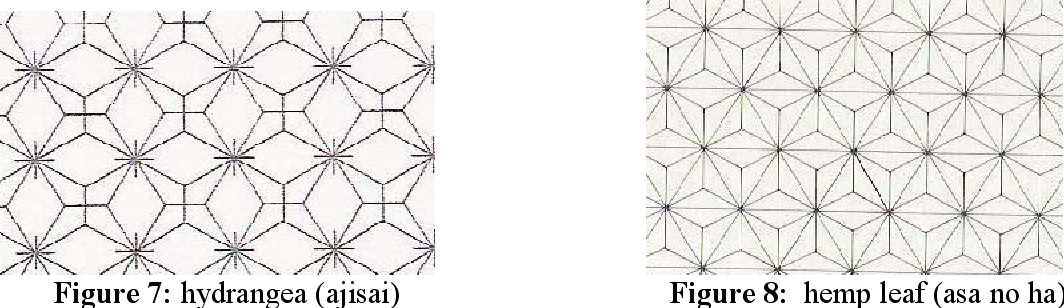
3.2 Hemp leaf motif. The hemp leaf motif may look similar to the hydrangea but there is a fundamental difference. It stems from the equilateral triangle. Here the triangular grid rules. Rows and rows of isosceles triangles make the foundation. Intermediary connecting lines go from the tips of the angles to its center. In sewing this pattern one stitches series upon series of straight parallel lines.

4. Patterns that Use Hidden Elements

4.1 Salient features. This group of patterns I find especially intriguing and satisfying. They have the grid lines, the short connecting line segments, the pivot points, but in addition they employ stealth. The lines disappear and reappear. Like a diving whale, it is difficult to discern the course. However, if one examines the base grid carefully and see where the lines fall, the underlying relationships and design strategies become apparent.

4.2 Counterweights. For this design motif one draws rows of circles tangent to one another on a square grid. Each circle would have a four-square diameter and a two-square radius. Next a second set of circles is drawn as an overlay with the same diameter/radius. The centers of these circles are in the exact middle of the space left void in the first set. If all the lines are sewn the design motif called Seven Treasures (shippo tsunagi) emerges. But for the counterweight design some arcs are eliminated. In the first set of circles only the NE and SW quadrants are stitched and in the second set, only the NW and SE quadrant get thread. When stitching the two sets are combined and the needle makes an undulating line diagonally across the cloth.

4.3 Plovers The plover or flock of 1000 birds depends on similar design strategies. Again the base is the square grid. The individual motif is six squares wide by six squares tall. First one establishes a baseline and draws a series of semicircles above and below that line using a radius of 1 square. A sashay of arcs emerges that are 1 square high by 2 squares wide. For the second baseline, one leaves three rows of squares free below the first baseline and uses the fourth line for the pivot point of the second row of arcs. The second undulating line should be parallel to the first one. This process is repeated until the entire design plane is complete. Next the cloth is turned 90 degrees and the second set of wavy lines with the same proportions are precisely overlaid upon the first. The tips match up perfectly. In stitching the needle follows the wavy lines across the fabric, selvage to selvage or down the bolt of material. Each individual motif has a four-block square free in the middle.

 

4.4 Connecting semicircles. This design is drawn with a base set of semicircles that is overlaid by a second set of smaller arcs. A series of semicircles are drawn above and below a baseline using a radius of 2 squares. The second baseline is 8 lines below the first. The second wavy line is parallel to the first. One fills up the design plane. Going back to the initial position one drawn a second set of wavy lines to mirror the first set. If calculations were accurate, this second set fits snuggly into the space left by the first set. One then turns the cloth 90 degrees and does the same operations. Now with the compass set with a .5 square radius, one draws smaller arcs subdividing the main arc. The resulting motif looks like a stylized bat to me.

5. Conclusion

There are many more patterns to discover and explore. In the Japanese textile tradition of sashiko stitching simple geometry elevates the plying of needle and thread to a celebrated, widely admired folk art. The simple task of mending took on a new meaning and importance. The cloth’s utility was extended and those white on blue fabrics beautified domestic life.

References

[1] Matsunaga, Karen Kim. Japanese Country Quilting. Tokyo: Kodansha International, 1990
[2] Parker, Mary. Sashiko. New York: Larks Books,1999.

 

Barbara Setsu Pickett
Department of Art
5232 University of Oregon
Eugene, OR 97403-5232, USA
email: bpickett@uoregon.edu