Abstract

This workshop originates in our collective exploration of how bodily knowledge in basket–weaving contributes to the understanding and learning about space and geometry. It has been designed to familiarize participants with the weaving of windmill loops and to explore how to use them to create surfaces with positive and negative curvature.
We start by constructing flat and curved surfaces by combining arrangements of windmill loops that include what we call ‘triangular corners’ and ‘pentagonal turns.’ Then we will explore the relationships between triangular corners, pentagonal turns, and positive or negative curvature. The final period will be dedicated to designing and making a free form curved surface by weaving windmill loops.

Introduction

This workshop is an outgrowth of work that we have conducted over the past six months in the context of a project entitled: “Forces in Translation. Basketry : Mathematics : Anthropology”. We investigate the interface between basketry, mathematics and anthropology, exploring how bodily knowledge in basket–weaving contributes to the understanding and learning about space and geometry, through the gestural moves we make and bodily skills we use. Our team includes basket weavers, anthropologists, mathematics educators, and researchers on the learning of mathematics. Beginning in September 2020, we organized an online studio for project staff that took place over the first week of November. This online studio was dedicated to learning about different techniques, including cycloidal looping, windmill knots, and triaxial weaving, as well as discussing concepts of topology and a selection of anthropological field studies. On the basis of our collective experiences in the online studio, we embarked on designing a two–day seminar open to the public. We conducted this seminar, attended by more than 50 participants, in January 2021.
Given the restrictions imposed by the lockdown, these were also online, and included working sessions as well as presentations and times for the sharing of experiences. Participants received, in advance, a set of materials to work with during the seminars, as well as prior to them and afterwards. During the second day, one of the activities involved working with windmill loops and windmill knots. The conversations and studio work on that day have inspired us to design this workshop centred on windmill loops and curvature. The main goals of this workshop are to familiarize participants with the weaving of windmill loops and to explore how to use them to create surfaces with positive and negative curvature.

The Plan

This 90–minute workshop will encompass three periods:

Period one (35 minutes)
Brief introduction to our project and voluntary sharing math/craft/art interests from the participants (10 min). Work with windmill loops to weave three units: a flat one, a triangular corner, and a pentagonal turning (15 minutes). Sharing work and observations (10 min).

Period two (20 minutes)
Study with sheets of paper the differences between zero, positive, and negative curvature, as generated by squared, triangular, and pentagonal holes. In order to make possible its completion in 20 minutes, this period will include demonstrations by instructors with materials prepared in advance.

Period three (35 minutes)
Create a surface with windmill loops combining flat units, triangular corners and pentagonal turnings.

 

Description of materials and activities for each period.

Getting to know windmill loops and the bending of a surface woven with them

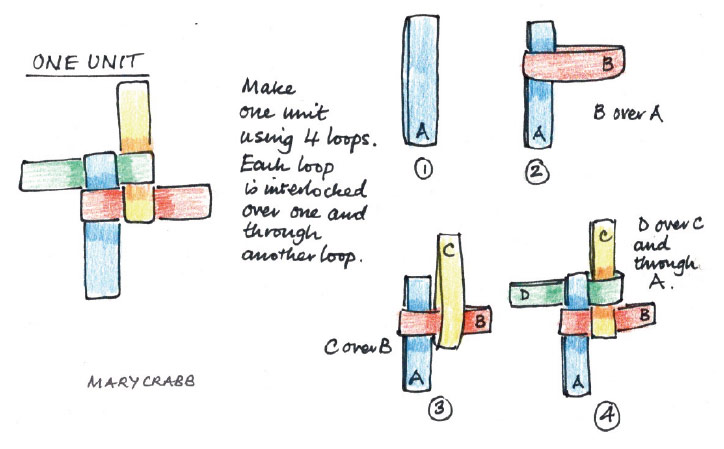
Figure 1: Making a single unit

After the introductory conversation, we will work with windmill loops. The supplementary section includes an instruction sheet on how to make the loops themselves. Each participant will need 40 loops. The first step will be to make a single unit with four windmill loops following the steps of Figure 1. Then we will practice joining units to create a flat surface (Figure 2). Next, we will make a triangular corner (Figure 3) and finally a pentagonal turning (Figure 4).

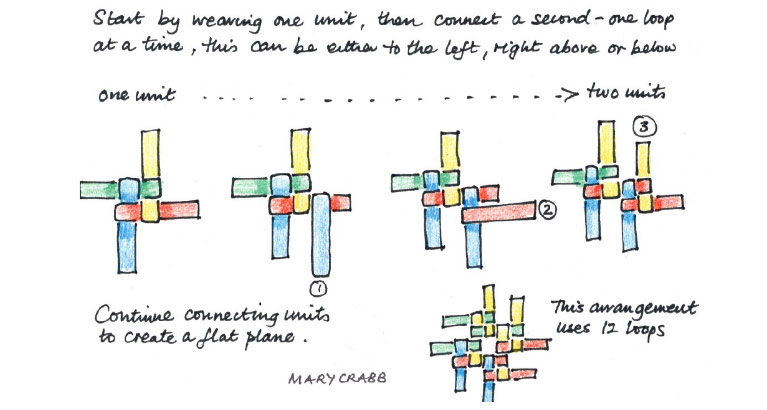
Figure 2: Connecting units

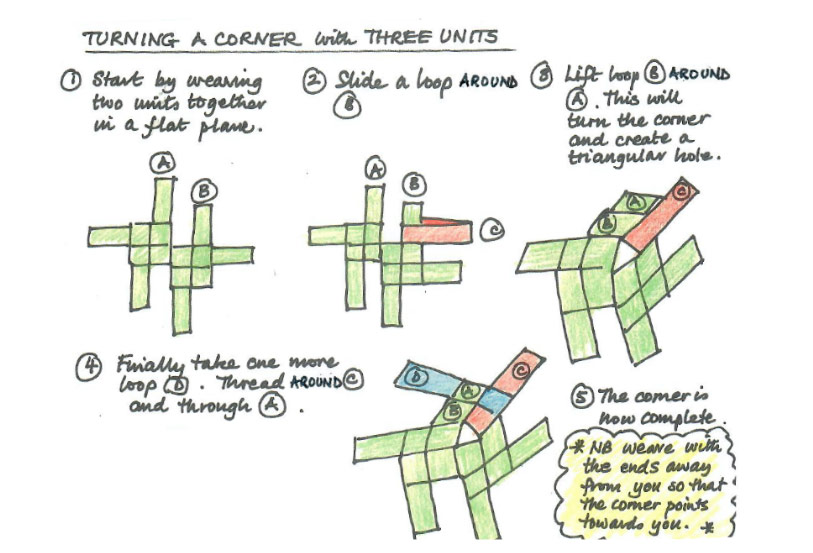
Figure 3: Turning a corner with three units

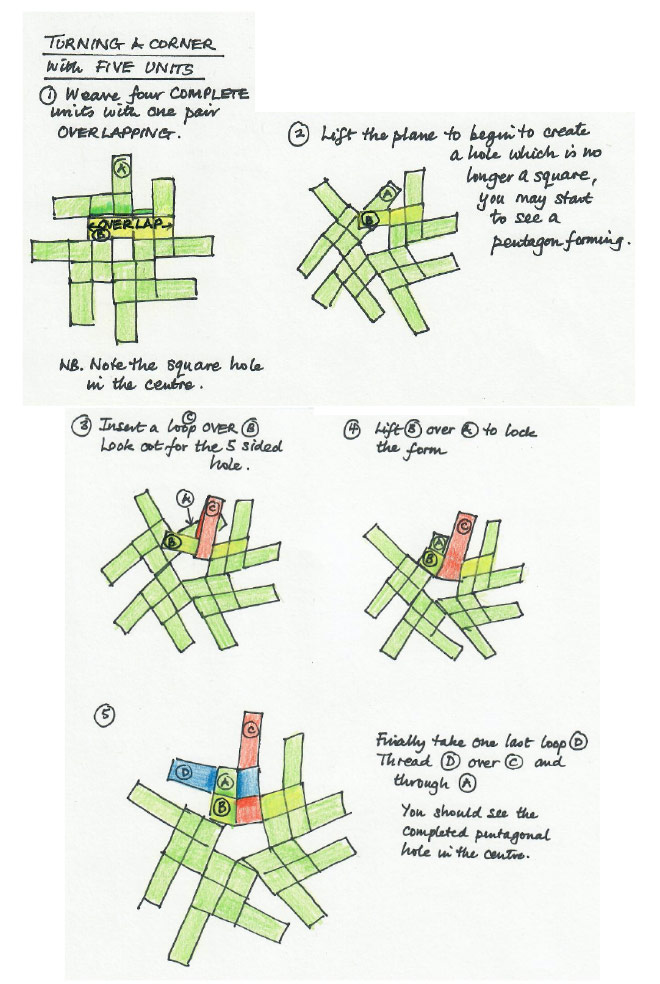
Figure 4: Turning a corner with five units

Curvature with triangular corners and pentagonal turns
This section describes how some participants came to make sense of how triangular corners and pentagonal turns generate curvature, which is only one of the many ways in which this can be achieved depending on the background and orientation of the craftworkers. Those interested in a general analysis of curvature based on the theorem of Gauss–Bonnet can consult Harriss [2], which is a creative pathway for grasping its meaning. In order to understand the generation of curvature by triangular corners and pentagonal turns with windmill loops, we worked with sheets of paper making square holes and then either eliminated or created
an additional side. Figure 5a and 5b show an example of each of these.

Figure 5: Positive and negative curvature from a square hole: (a) by transforming it into a triangular hole and (b) by transforming it into a pentagonal hole. Creating a cone: (c) by cutting out 45°, and (d) by cutting out 135°

Our first observation was that the generated surface curvature depends on the angle added or eliminated from the original square. In Figure 5a we can see that the triangular hole keeps two original right angles from the square and replaces the other two with an angle smaller than 180°. In other words, we have created an angular “deficit” with respect to the original 360° summed up by the internal angles of the square. In Figure 5b we kept the four right angles of the original square and added a fifth one, which involved the creation of an angular “excess” with respect to the original 360°. The second observation was that a triangular hole generated a positive curvature — a ball-like one — and the hexagonal hole a negative curvature — a saddle-like one. Additional examples, starting with original holes different from squares, showed that an angular deficit always correspond to positive curvature and an angular excess to negative curvature. We had started with squares because this is what our weaving of windmill loops created, but if we started from say, a hexagon, converting it into a pentagon would create positive curvature and into a heptagon a negative curvature. This experimentation led us to realize that what really matters is the angular span of the taken-out material (Figure 5a) or added material (Figure 5b). The significance of the hole is not just its shape, but also providing flexibility of the subsequent joining. Figure 5c shows how constrained we are to form a triangular corner without the hole. This prompted us to think about differences between vertical cones (Figure 5c), such that the apex is along a perpendicular line from the centre of the base, and oblique cones (Figure 5d).

By combining triangular corners and pentagonal turns, we began to create arbitrarily curved surfaces. Figure 6 shows a single page on which we made three square holes. Two of them were converted into triangles and the third one, at the centre of the page, into a pentagon. We can see positive curvature surrounding the triangles and negative curvature surrounding the hexagon.

Figure 6: Combining triangular corners and pentagonal turns

Eventually we could create closed shapes whose overall curvature would add up to the ones created by triangular corners and pentagonal turns. Figure 7 shows a traditional form, a dog, which is originally described in the only reference we have found about windmill loops [1]. It was made by Mary Crabb by weaving triangular corners and pentagonal turns.

Figure 7: Dog woven with windmill loops. Note the triangular corners and pentagonal turns in areas of positive and negative curvature.

Designing surfaces with curvature
In this third period participants will design and begin to make a curved surface by weaving windmill loops and combining triangular corners and pentagonal turns. As time allows, participants may complete their surface afterwards. This surface may be designed to resemble a particular shape, such as a ball or a dog, or be free form.

References
[1] C. Fleming. “Mack the Scottie from the Isle of Wight.” Stage and Screen Specialities, 1988, Number 12.
[2] E. Harriss. “Gauss-Bonnet Sculpting.” Bridges Conference Proceedings, 2020, pp. 137–144.
http://archive.bridgesmathart.org/2020/bridges2020-137.html

Stephanie Bunn sjb20@st–andrews.ac.uk; Hilary Burns hilary@basketryandbeyond.org.uk; Mary Crabb mary@marycrabb.co.uk; Geraldine Jones; Charlotte Megroureche charlottemegroureche@gmail.com; Ricardo Nemirovsky r.nemirovsky@mmu.ac.uk