I came across this complicated looking but simple paper structure and have been happily playing around with it for days.

I’ve been able to locate only once source for these, which is at http://hattifant.com/triskele-paper-globes-flower-edition/, an exquisite site by German artist Manja Burton. Fact is, her site has enough about these globes that, really, no one else needs to ever write about them again ever, but, oh well, here I go.

Manja calls these Triskele Globes. I have no idea whether these are a traditional paper-folding design, or if she developed it herself. “Triskele” is a symbol which depicts three interlocking spirals. These paper globes appear to be interlocking spirals, but the spiraling is simply a wonderful illusion.

Bonus Update: just as I was about to hit the Publish button for this post, I received a note from Manja, responding to my questions about this structure. I’ve added her response at the end of the post.

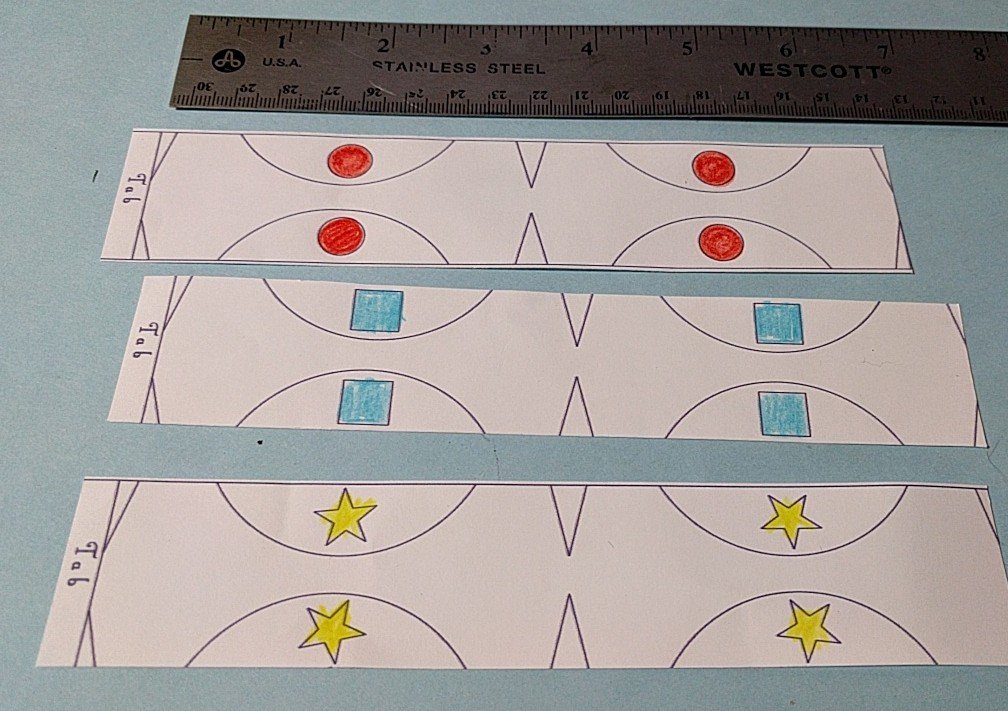Three rectangles that will become globes

The globes are made with three interlocking strips.

After interlocking the strips, the arcs are folded in. It really helps to pre-score the curved fold lines. Here’s a short video at https://youtu.be/m4W1hT1hnF4?si=UjOlnJvao3YQmeNo

---

If you don’t have access to a copy machine, it’s absolutely possible to construct your own template for these paper strips. Here’s a grid that can be used to understand the proportions of the shapes.

The paper strips for the Spiraling ornament, mapped on a grid. The strips are 48 squares tall (plus two more for the tab), 10 square wide, and the circles have an a radius of 8 squares, but only 1/3 of the circle is on the paper strip. There, that should get you started.

 

---

• I’ve had such a great time with these. I’m surprised every time I see the transformation happen as the strips of paper become a spiraling globe.
• Make them into dice, fortune tellers, add quotes.

---

Here’s the bonus update: I wrote a note to Manja which said.

Manja, I am enchanted by the Triskele balls, and am currently writing a blog post about them, which will include links to your site. Can you tell me something about history of these balls? did you invent the form or did you come across it in your travels? Many thanks for your beautiful work.

She wrote back, saying:

It is a couple of years back now that I saw an image of one of these globes and all I knew was that it was made out of three strips of paper. I spent a whole day on figuring out how it works… I never found that picture again online. I did do some more research on it back then and couldn’t find anything. So I asked the Hattifant community to help me find a name. And that was absolute fun and we in the end came up with Triskele Paper Globes.  Today, I have seen more of them and also in the Scandinavian area… there they seem to be called “click balls”. So please I would love to know more, too!  If you find out more do let me know!”
Okay! If anyone knows something about the history of these balls, let us know!

---

 

Addendum, December 18.2018

After reading my post about these ornaments a twitter friend examined the curves and came up with some tweeks https://twitter.com/mathforge/status/934826360970924033

Then this friend, who I know only by the name Loop Space wrote a great post for the mathematically curious which is https://loopspace.mathforge.org/CountingOnMyFingers/Triskele/. I especially like how   Loop Space illustrated the explanation.

 

---

A couple of weeks ago I found this blog post via Pinterest:

http://heartheartseason.blogspot.ca/2015/12/baubles-that-go-plop.html

The post is about a month earlier than the one you found. The author makes no claim to have invented the globe structure, so perhaps it is traditional. ; ]

---

 

One of my twitter friends informed me that they configuration of the loops is called Borromean Rings. More about that is at http://www.jasoncantarella.com/wordpress/images-of-borromean-rings-and-tight-clasp/

---

DEAN FRATE
May 13, 2019
I was totally captivated by the globes, and “had” to make some. So, I did. Then, I saw your link to the LoopSpace post and it captured my inner math geek. I took your template and the LoopSpace template and re-created them in Illustrator, layering for print-and-cut on my Sillhouette.

I found what I expected. The LoopSpace template cut a very precise curve that set a bit more true and straight on the face of the inner cube under it. It totally appealed to my sense of precision. However, I found it impossible to complete without wrinkles, or bulges, or crimps where the curves fold down. It was too precise to allow enough wiggle room for my human fingers to work. I needed less precise tolerances to make a better looking sphere.

In the end, I modified your template a bit, added graphic “drop zones”, and set the layers to make decorating and cutting easily repeatable. I’m looking forward to making a few different versions…on my next day off.

Paula Beardell Krieg
May 15, 2019
Dean, thanks so much for this comment. I was very interested in your exploration. When I saw LoopSpace’s template I tried it out immediately. The reasoning behind this work made sense to me but, like you, I found that it didn’t fold the way that I wanted it to. I had wondered if I was too impatient when I had done it, which sometimes happens when I get a bit overly excited about what I’m working on. But, since you had the same experience with the folding as I had, I have been thinking about this some more. I don’t think there’s an error in the math or in our technique, rather, I’m thinking that, even though the math checks out, the structure becomes skewed by the fact that the paper has thickness. This happens lots in structures I make: I do the math just right, but paper thickness adds an elements that is hard to add into my calculations. So I make adjustments as I work with the materials.

---

 

Jürgen Reimann
August 25, 2019
Thanks for sharing – I am currently designing a score board for easier scoring of the arcs and always thought that the original circular arcs might not be the perfect solution – now that I got the optimized curve that you provided in the link above I made a prototype globe and realized that the shape is much smoother now. Kind regards, Jürgen